The Triangle Question

I’m currently entertaining myself by working through the Ruby Koans which I’d somehow missed over the last few years.

Most of the questions are fairly mundane like

def test_iterating_with_each
  array = [1, 2, 3]
  sum = 0
  array.each do |item|
    sum += item
  end
  assert_equal __, sum
end

but the “Triangle question is a bit of fun. You’re given a test like:

class AboutTriangleProject < Neo::Koan
  def test_equilateral_triangles_have_equal_sides
    assert_equal :equilateral, triangle(2, 2, 2)
    assert_equal :equilateral, triangle(10, 10, 10)
  end

  def test_isosceles_triangles_have_exactly_two_sides_equal
    assert_equal :isosceles, triangle(3, 4, 4)
    assert_equal :isosceles, triangle(4, 3, 4)
    assert_equal :isosceles, triangle(4, 4, 3)
    assert_equal :isosceles, triangle(10, 10, 2)
  end

  def test_scalene_triangles_have_no_equal_sides
    assert_equal :scalene, triangle(3, 4, 5)
    assert_equal :scalene, triangle(10, 11, 12)
    assert_equal :scalene, triangle(5, 4, 2)
  end
end

and told to implement the triangle method

# Triangle Project Code.

# Triangle analyzes the lengths of the sides of a triangle
# (represented by a, b and c) and returns the type of triangle.
#
# It returns:
#   :equilateral  if all sides are equal
#   :isosceles    if exactly 2 sides are equal
#   :scalene      if no sides are equal
#
# The tests for this method can be found in
#   about_triangle_project.rb
# and
#   about_triangle_project_2.rb
#
def triangle(a, b, c)
end

# Error class used in part 2.  No need to change this code.
class TriangleError < StandardError
end

I started typing if a == b… but quickly realised that there was no branching logic needed at all. All the triangle method needed to do count the number of unique sides so instead of a messy conditional statement like

if (a==b and a==c)
  value = :equilateral
else
  if (a==b or a==c or b==c)
    value = :isosceles
  else
    value = :scalene
  end
end

…we can just say:

def triangle(a, b, c)
  sides = [a, b, c]
  unique_sides = sides.uniq.length
  types = [nil, :equilateral, :isosceles, :scalene]
  types[unique_sides]
end

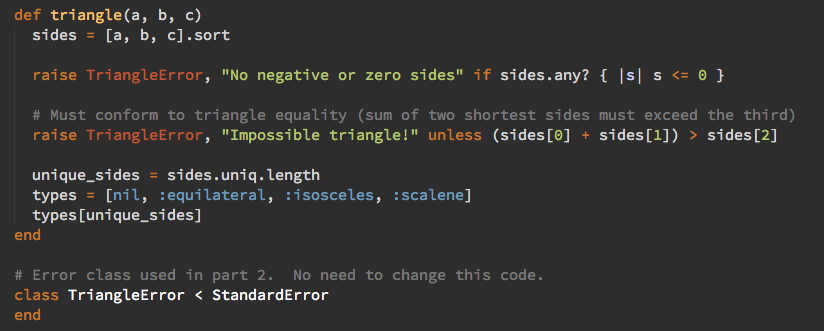
This uses the number of unique sides as the array index to determine the triangle type. Even adding the error checking required later, can be done without messy conditionals:

def triangle(a, b, c)
  sides = [a, b, c].sort

  raise TriangleError, "No negative or zero length sides" if sides.any? { |s| s <= 0 }

  # Must conform to triangle equality (sum of two shortest sides must exceed the third)
  raise TriangleError, "Impossible triangle!" unless (sides[0] + sides[1]) > sides[2]

  unique_sides = sides.uniq.length
  types = [nil, :equilateral, :isosceles, :scalene]
  types[unique_sides]
end

I think this would make a good interview question. Not because it’s particularly hard or tricky (interview questions shouldn’t be) but because there are multiple ways to solve it and it encourages a good discussion.

How could we rewrite if a <= 0 || b <= 0 || c <= 0 using a block? What are the disadvantages of my array indexing approach? How would you rewrite it to use a case…when structure?

Note: The Koans are about learning and enlightenment and are not a test. Don’t set them all as interview test — they’re too long, and easy to “cheat” because the test suite will give you the next expected answer. This triangle question could be extracted though. Also, setting up a Nitrous.io instance for your candidate means they don’t have to set anything up on their own machine.

Jamie Lawrence

The Triangle Question